Constructing Efficient Simulated Moments Using Temporal Convolutional Networks

Jonathan Chassot and Michael Creel

Deep Learning for Solving and Estimating Dynamic Models
(DSE2023CH)

August 24, 2023

Our Contribution

  • Propose a method to estimate model parameters leveraging deep learning
  • Allow for inference using well-established econometric methods
  • Provide an exactly identifying and informative set of statistics for simulation-based inference
  • Achieve performance equal to or better than maximum likelihood for small and moderate sample sizes for several DGPs

Motivating Example

  • Parameter estimation for a complex data-generating process (DGP)
  • Failure of traditional estimation methods (ML, GMM)

Motivating Example

  • Parameter estimation for a complex data-generating process (DGP)
    • Presence of latent variables
    • High-dimensional integrals
    • …
  • Failure of traditional estimation methods (ML, GMM)
    • Intractable likelihood
    • Computational constraints
    • No closed-form theoretical moments

→ Use simulation-based inference methods

Methodology

Simulation-based Inference

Match sample statistics with statistics obtained through simulation

Method of Simulated Moments

  • Use simulated moment conditions instead of theoretical ones
  • Match data moments and simulated moments
$$ \hat{\theta}_{\text{MSM}} = \underset{\theta \in \Theta}{\arg \min} \ \left(T^{-1}\sum_{t=1}^T m(x_t, \theta)^{\top}\right) W_T \left(T^{-1}\sum_{t=1}^T m(x_t, \theta)\right), $$

where $W_T$ is a weighting matrix and

$$m(x_t, \theta) = f(x_t) - \frac{1}{S} \sum_{s=1}^S f(\tilde{x}_t(\theta))$$

with $S$ the number of simulations and $\tilde{x}_t(\theta)$ the data simulated at parameter $\theta$.

Method of Simulated Moments

  • …but how do we choose $f(\cdot)$ in
$$m(x_t, \theta) = f(x_t) - \frac{1}{S} \sum_{s=1}^S f(\tilde{x}_t(\theta))$$

Optimal Moment Conditions

  • Choosing optimal moment conditions is difficult
  • Overidentification leads to high asymptotic efficiency but also to high bias and/or variance in finite samples (Donald, Imbens & Newey, 2009)

Optimal Moment Conditions

  • Choosing optimal moment conditions is difficult
  • Overidentification leads to high asymptotic efficiency but also to high bias and/or variance in finite samples (Donald, Imbens & Newey, 2009)

Theory:

  • Gallant & Tauchen (1996) show that the optimal choice of moment conditions corresponds to the score function (equivalent to MLE)

Optimal Moment Conditions

  • Choosing optimal moment conditions is difficult
  • Overidentification leads to high asymptotic efficiency but also to high bias and/or variance in finite samples (Donald, Imbens & Newey, 2009)

Theory:

  • Gallant & Tauchen (1996) show that the optimal choice of moment conditions corresponds to the score function (equivalent to MLE)

Practice:

Optimal Moment Conditions

Goal:

  • Given a data set $\{x_t \mid x_t \in \mathbb{R}^k\}_{t=1}^T$, generated by our DGP under true parameter value $\theta_0$, we would like to find $f(x_t) \approx \theta_0$

Optimal Moment Conditions

Goal:

  • Given a data set $\{x_t \mid x_t \in \mathbb{R}^k\}_{t=1}^T$, generated by our DGP under true parameter value $\theta_0$, we would like to find $f(x_t) \approx \theta_0$

Idea:

  • Generate samples $\{\tilde{x}_t(\theta) \mid \tilde{x}_t(\theta) \in \mathbb{R}^k\}$ with $\theta \in \Theta$ and use deep learning to infer $f(\cdot)$, a mapping from data to parameters

Neural Networks

  • Long Short-Term Memory Networks (LSTM)
  • Temporal Convolutional Networks (TCN)

Neural Networks

  • Long Short-Term Memory Networks (LSTM)
  • Temporal Convolutional Networks (TCN)
    • Introduced as WaveNet (van den Oord et al., 2016)
    • Fully parallelizable
    • Flexible receptive field size
    • Serve as the main model in this work

Benchmark Results

Results for Simple DGPs

  • Benchmark our TCNs and LSTMs against MLE for 3 data-generating processes (MA(2), Logit, GARCH(1,1)) where the likelihood is tractable
  • Sample sizes 100, 200, 400, and 800
  • Comparison across 5'000 test samples for each setting
  • Conjecture: if the neural networks do well, they will also perform well when the MLE is not available

Jump-Diffusion Process

Jump-Diffusion Stochastic Volatility

$$ \begin{align*} dp_{t} & =\mu \, dt+\sqrt{\exp h_{t}} \, dW_{1t}+J_{t} \, dN_{t}\\ dh_{t} & =\kappa(\alpha-h_{t})+\sigma \, dW_{2t} \end{align*} $$

Jump-Diffusion Stochastic Volatility

$$ \begin{align*} dp_{t} & =\mu \, dt+\sqrt{\exp h_{t}} \, dW_{1t}+J_{t} \, dN_{t}\\ dh_{t} & =\kappa(\alpha-h_{t})+\sigma \, dW_{2t} \end{align*} $$
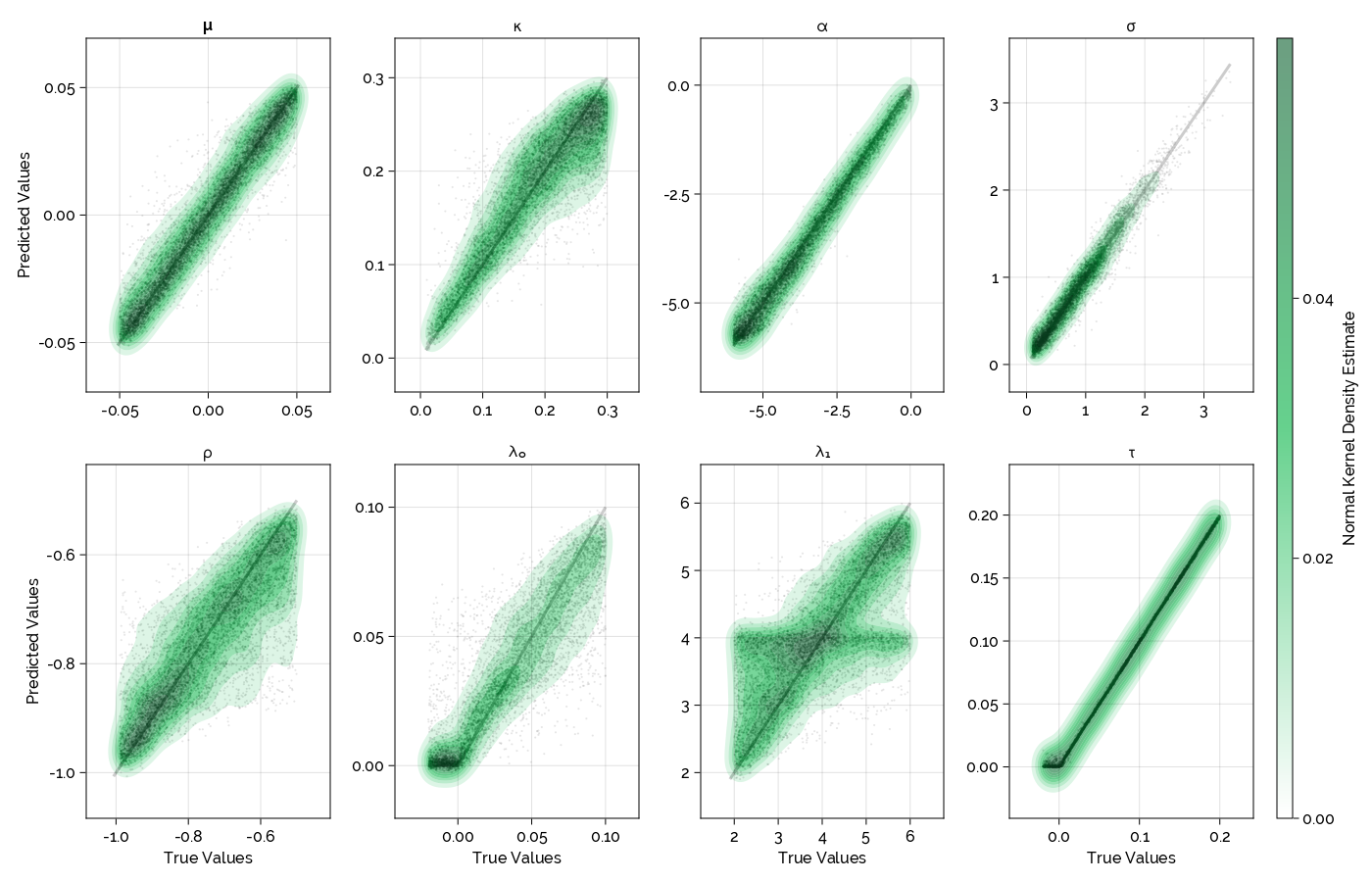
  • $p_t$: logarithmic price
    • $\mu$: average drift in price
    • $J_t$: jump size ($J_t = a \lambda_1 \sqrt{\exp h_t}$) with $\mathbb{P}[a=1]=\mathbb{P}[a=-1]=\frac{1}{2}$
    • $N_t$: Poisson process with jump intensity $\lambda_0$
  • $h_t$: logarithmic volatility
    • $\kappa$: speed of mean-reversion
    • $\alpha$: long-term mean volatility
    • $\sigma$: volatility of the volatility
  • $W_{1t}, W_{2t}$: correlated Brownian motions with correlation $\rho$

Jump-Diffusion Stochastic Volatility

Parameters:

  1. $\mu$: average drift in price
  2. $\kappa$: speed of mean-reversion
  3. $\alpha$: long-term mean volatility
  4. $\sigma$: volatility of the volatility
  5. $\rho$: correlation between $W_{1t}$ and $W_{2t}$
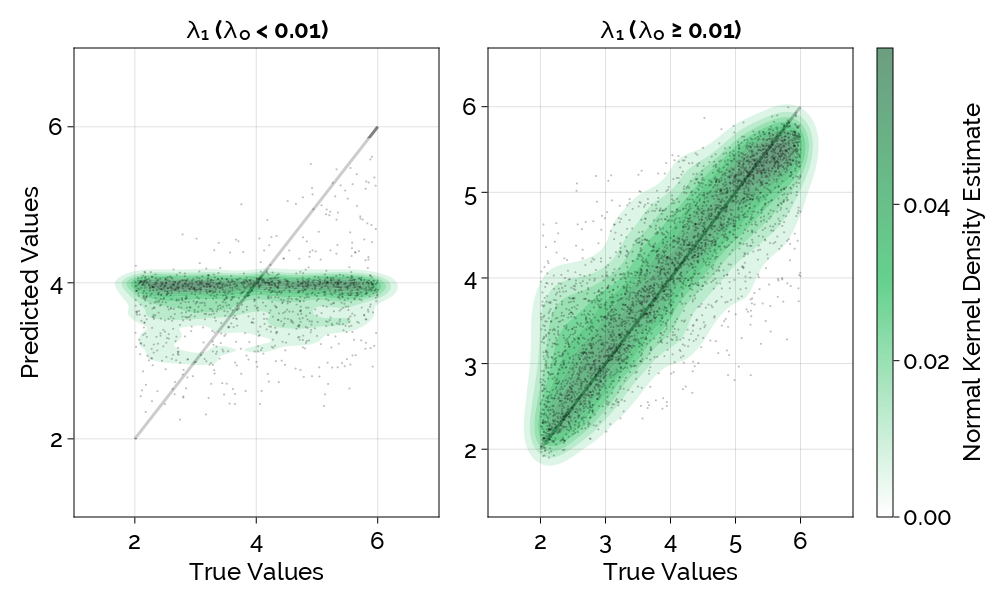
  6. $\lambda_0$: jump intensity
  7. $\lambda_1$: jump magnitude
  8. $\tau$: the volatility of a measurement error $N(0, \tau^2)$ added to the observed price

Observables:

  1. logarithmic returns
  2. realized volatility
  3. bipower variation

Conclusion

Conclusion

  • Best case scenario for deep learning
  • Once the network is trained, inference is as fast as matrix multiplication
  • Limited only in the cost of simulation
  • Promising results on three simple DGPs and one moderately complex DGP
  • Easy to implement